Применения физики плазмы весьма многочисленны. Работа ртутных выпрямителей, газотронов, газоразрядных источников света основана на использовании той или иной формы газового разряда и, следовательно, предполагает получение плазмы с заданными параметрами. Существует однако, одна область применения физики плазмы, которая занимает совершенно особое место. Речь идет об управляемом синтезе легких ядер. Это исключительная по трудности техническая задача, и мы находимся здесь еще очень далеко от достижения желаемой цели. Вместе с тем значение этой проблемы столь велико, что, несмотря на отсутствие особенно крупных успехов, над попытками ее решения работают многочисленные коллективы физиков во многих странах. В свою очередь, и это мы отметили в начале главы, поиски решения проблемы управляемого синтеза, наряду с развитием космических исследований, сыграли основную роль в быстром прогрессе физики плазмы, который происходит с середины текущего столетия. Остановимся, в общих чертах, на важнейших аспектах этого вопроса.
Прежде всего следует пояснить, в чем состоит цель проводимых исследований. Решение проблемы управляемого синтеза означает получение неограниченного по мощности, доступного и дешевого источника энергии. Сырьем должен служить дейтерий, запасы которого в мировом океане практически неисчерпаемы. Разумеется, речь идет о перспективах на будущее, так как помимо далеких от исчерпания запасов угля и нефти мы только приступили к эксплуатации обычного ядерного горючего, урановых и ториевых руд. Но темпы роста энергопотребления во всем мире столь велики, что поиски новых источников энергии должны начинаться уже сейчас.
Среди различных экзотермических реакций слияния в процессе которых из легких ядер синтезируются более тяжелые, особенно интересными являются реакции соединения ядер дейтерия и трития. Кулоновское отталкивание приводит к тому, что вероятность ядерных реакций между заряженными частицами оказывается достаточно большой только при значительной энергии сталкивающихся частиц. Это же обстоятельство заставляет при выборе реагирующих веществ ограничиваться элементами с малым порядковым номером. В результате практический интерес представляют только две названные реакции:
D+D -> He3 + n +3,25 Мэв (D+D -> T + p + 4 Мэв)
D+T -> He4 + n + 17,6Мэв
Обе реакции в свое время были подробно исследованы в ходе экспериментов, при которых мишень, содержащая дейтерий или тритий, подвергалась бомбардировке пучками дейтонов, ускоренных до энергии в несколько десятков кэв. Получаемый в этих условиях энергетический выигрыш (энергия продуктов реакции составляет несколько Мэв, тогда как на ускорение дейтона затрачиваются только десятки кэв), однако, иллюзорен, так как в ядерные реакции вступает лишь очень малая доля (~10-4) ускоренных дейтонов. Подавляющая масса дейтонов растрачивает накопленную энергию маленькими порциями, производя возбуждение и ионизацию атомов, т. е. в конечном счете просто нагревая мишень. Это происходит потому, что сечения ядерных реакций несравненно меньше сечений возбуждения и ионизации. Выход состоит в проведении реакции в полностью ионизованной горячей водородной плазме. В этом случае потери на возбуждение и ионизацию исключены и столкновения между ионами плазмы рано или поздно завершаются ядерным синтезом.
Пусть температура плазмы T и концентрации взаимодействующих частиц n1 и n2. Если скорость данного иона относительно второго есть v1,2, то вероятность того, что данный ион прореагирует за 1 секунду с каким-либо из ионов второго рода, дается выражением
Lv1,2n2
Здесь L- эффективное сечение реакции синтеза, величина, быстро растущая со скоростью. Если бы все n1ионов первого рода обладали одной и той же скоростью v1,2, то общее число реакций, происходящих в 1 см3плазмы за 1 сек, определялось бы равенством:
R1,2= n1n2Lv1,2
При заданной температуре произведение должно быть усреднено по максвелловскому распределению. Обозначая через e энергию, выделяющуюся при каждом акте реакции, получим выражение для удельной мощности в виде
w=n1n2e<Lv> (1)
Зависимость L(v) для рассматриваемых реакций известна, следовательно, величина <Lv> может быть вычислена, а вместе с ней может быть найдена и удельная мощность w при любой температуре и плотности плазмы.
Численные оценки показывают, что величина w быстро растет с температурой; при температуре "горения" в несколько сотен миллионов градусов и при плотности плазмы ~1015 см-3 она составляет около 105 квт/м3. Повышение температуры и плотности приводит к более энергонапряженным режимам, при которых должны прогрессивно возрастать технические трудности в реализации проекта. Более "мягкие" режимы приводят, при не слишком малой общей мощности термоядерного реактора, к очень большим размерам системы. Таким образом, взятые значения в представляют собой разумный технический компромисс между противоречивыми требованиями. Заметим еще, что использованные оценки относятся к дейтериевой плазме; для равнокомпонентной смеси дейтерия и трития оптимальные "рабочие" температуры ниже.
Далее возникает следующий естественный вопрос: каким образом могут быть созданы указанные условия в зоне реакции? Точнее: как нагреть плазму до необходимых чрезвычайно высоких температур и как удержать нагретые частицы от разлета в течение времени, достаточного для протекания ядерных реакций? Главная трудность связана, по-видимому, со второй частью вопроса. Энергия, которая должна быть сообщена заданному объему плазмы с известной плотностью для ее нагревания до 108 K, представляет собой весьма скромную величину; она равна энергии, которую надо затратить, чтобы нагреть такой же объем воды всего на 1 K. Напротив, потоки частиц (и тепла) от зоны реакции к периферии будут огромны. Если воспользоваться формулами кинетической теории газов и значением длины пробега для водородной плазмы из формулы (1), то после подстановки численных значений констант мы получим следующее выражение для потока тепла от нагретой области к холодной стенке:
q = 10-6 T7/2 x эрг/см2сек (2)
здесь x- толщина переходного слоя. При температуре 108 К и протяженности слоя 1 км (!) поток тепла достигает гигантской величины 107 квт/см2. Необходимость эффективного удержания частиц в зоне реакции очевидна.
Основная идея, которая определила путь исследования проблемы управляемого синтеза, состоит в использовании принципа магнитной термоизоляции. В Советском Союзе эта идея была высказана еще в 1950 г. А. Д. Сахаровым и И. Е. Таммом.
В предыдущем параграфе было показано, что коэффициент диффузии, а вместе с ним и коэффициент теплопроводности уменьшается на много порядков величины, если перемещение частиц происходит в направлении, перпендикулярном к сильному магнитному полю. Поэтому, если зона реакции отделена от стенок сильным магнитным полем, то можно надеяться на радикальное сокращение тепловых потоков и построение термоядерного генератора перестает казаться беспочвенной утопией. Тот же результат можно сформулировать в других терминах, если вспомнить, что плазма является диамагнетиком. Тогда, если поле внутри плазмы отсутствует, величина удерживающего поля может быть представлена в виде:
H2/8Pi=n*k*(Te+Ti) (3)
Для плазмы с выбранными параметрами (n~1015 см-3, T~108 K), необходимое для удержания поле должно составлять 25-30 килоэрстед. Эти большие величины отнюдь не выходят за пределы технических возможностей.
Мы говорим все время о теплопередаче в плазме поперек магнитного поля, но не следует забывать, что тепловые потоки вдоль силовых линий магнитного поля остаются незамагниченными; необходимо затруднить уход частиц и в этом направлении. Здесь открываются три возможности. Первая из них нам, в сущности, уже знакома: она состоит в помещении плазмы в магнитную ловушку, т. е. в магнитное поле такой конфигурации, где оно усилено в областях ухода силовых линий из зоны реакции, в районе их пересечения со стенками; Вторая возможность состоит в ликвидации открытых концов силовых линий путем их сворачивания в кольцо. Наконец, третий путь состоит в использовании плазмы с относительно большой плотностью и в настолько быстром ее нагревании, что за время ухода вдоль силовых линий основная масса частиц успевает испытать ядерные столкновения.
Первая схема термоизоляции полностью себя оправдывает, если речь идет об удержании столь редкой плазмы, что ее можно рассматривать как собрание отдельных частиц. Большие времена жизни частиц в радиационных поясах Земли естественного и искусственного происхождения служат хорошим примером сказанному. Однако, в лабораторных опытах, выполненных с более плотной плазмой, т. е. в условиях, когда могут проявляться коллективные взаимодействия, обнаружились серьезные трудности. Времена жизни плазмы оказались на много порядков величины меньшими тех, которые можно было ожидать в результате столкновений плазменных частиц между собой или с молекулами остаточного газа и последующего ухода в конус потерь. Фактически времена жизни плазмы в некоторых моделях открытых ловушек составляли около 100 микросекунд (при плотности плазмы около 10-9 см-3), тогда как времена жизни, обусловленные уходом в конус потерь, должны были измеряться минутами.
Этот результат качественно станет яснее, если учесть, что плазма, как всякий диамагнетик, должна выталкиваться из области более сильного поля. С этой точки зрения механизм действия магнитных пробок, удерживающих плазму внутри ловушки, вполне понятен. Но в ловушках рассматриваемого типа имеются также области, где поле убывает по мере удаления от оси по радиусу; здесь можно ожидать развития неустойчивости - появления плазменных "языков" или "желобков", перемещающихся поперек поля и переносящих плазму в сторону меньших значений поля. И действительно, прямые эксперименты указали на существование в этих ловушках неустойчивости "желобкового" типа, которая ограничивает время жизни плазмы.
Существенный прогресс наметился в 1961 - 1962 гг., когда были построены ловушки с более сложной топографией магнитного поля. В этих системах, помимо нарастания поля к пробкам, увеличение поля обеспечивается и в радиальном направлении с помощью ряда стержней, по которым пропускаются сильные токи чередующегося направления. В таких ловушках желобковая неустойчивость оказалась подавленной, и были получены плазменные конфигурации с плотностью 109 - 1010 см-3 и временем жизни в десятки миллисекунд.
На рис. 1 показано, как меняется измеренное на опыте время жизни в зависимости от величины a радиального пробочного отношения , т.е. величины 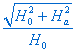 , где H0 - значение поля в центре ловушки, Ha - азимутальная составляющая поля на периферии, обусловленная током, текущим по стержням. Резкий подъем кривой (масштаб по оси ординат - логарифмический) приходится на то значение a, начиная с которого абсолютное значение поля на периферии делается больше значения поля на оси системы.
, где H0 - значение поля в центре ловушки, Ha - азимутальная составляющая поля на периферии, обусловленная током, текущим по стержням. Резкий подъем кривой (масштаб по оси ординат - логарифмический) приходится на то значение a, начиная с которого абсолютное значение поля на периферии делается больше значения поля на оси системы.
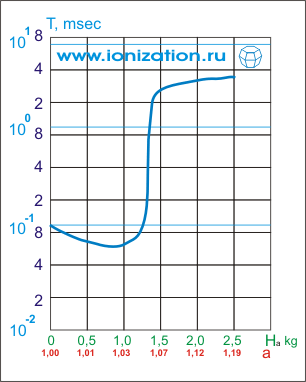
Дальнейшее повышение плотности плазмы сопровождается появлением новых видов неустойчивости, но к настоящему времени эти трудности удалось преодолеть по крайней мере до плотностей 1011 см-3 путем увеличения радиального пробочного отношения. На рис. 2 приведена фотография модели ловушки с комбинированным магнитным полем, построенной М. С. Иоффе в Институте атомной энергии в 1967 г.

Перейдем к обсуждению второй схемы. Замыкая силовые линии, мы естественным образом приходим к установка типа кольцевого соленоида. Теперь магнитное поле повсюду ориентировано параллельно стенкам, и частицам, чтобы покинуть систему, надо двигаться поперек силовых линий. Но магнитное поле внутри тора слегка неоднородно, оно спадает к внешней стенке тора, что вызывает дрейф частиц. Как мы знаем, дрейф в неоднородном магнитном поле происходит по нормали к направлению основного поля и к направлению его градиента и зависит от заряда частиц. Если ионы дрейфуют к верхней стенке тора, то электроны будут оседать на дно (рис. 3). Разделившиеся заряды создадут электрическое поле, и плазма, тем или иным способом образованная внутри тора, начнет, как целое, дрейфовать в скрещенных электрических и магнитных полях. Легко проверить, что окончательным итогом будет перемещение плазмы к внешней стенке тора.
Для компенсации этого дрейфа плазмы существуют различные способы. Можно пропускать через плазму продольный кольцевой ток, можно специальным образом усложнить соленоидную обмотку или, скрутив тор, придать магнитной системе форму восьмерки. Топография магнитного поля во всех этих случаях меняется радикально.
Здесь необходимо некоторое пояснение. Простейшие магнитные поля - постоянного магнита, прямого тока плоского контура, приводят как известно, в силу уравнения div B=0 к привычным картинам замкнутых силовых линий или линий, уходящих на бесконечность. Существует, однако, третья возможность, фактически наиболее общая: силовые линии могут оставаться в ограниченной области пространства, не замыкаясь и не уходя на бесконечность.
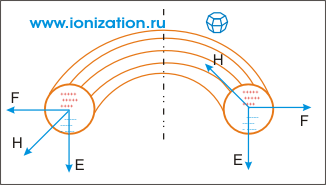
В приведенных примерах в результате деформации тороидальной магнитной системы и происходит преобразование замкнутых силовых линий - колец - в бесконечные силовые линии, непрерывно обвивающие кольцевую тороидальную ось и формирующие так называемые магнитные поверхности. Силовые линии, проходившие на различных расстояниях от оси тора, порождают (в простейшем случае) совокупность вложенных друг в друга коаксиальных магнитных поверхностей. В результате любая точка сечения тора оказывается соединенной с любой другой точкой сечения (равноудаленной от оси) силовой линией, принадлежащей к той или иной магнитной поверхности. Это означает, что перераспределение зарядов по сечению может осуществляться не поперек магнитного поля, а вдоль силовых линий. Поэтому накопление разноименных зарядов, а следовательно, и дрейф в скрещенных полях оказываются исключенными.
Варианты тороидальных систем с продольным током начали разрабатываться в Советском Союзе (установки типа "Токамак"), два других направления начали исследоваться в США (установки типа "Стелларатор"). Это большие и сложные инженерные сооружения. Так, одна из последних моделей Токамаков, установка T-3, представляет собой тороидальную камеру с большим диаметром 200 см и малым диаметром 40 см (рис. 4).

Продольное магнитное поле создается восемью катушками и может достигать 36 кэ. Катушки питаются ударным генератором с импульсной мощностью 75000 ква. Вакуумные условия превосходны: начальное давление остаточных газов около 10-8 мм рт. ст. Камера Токамака надета на железный сердечник и возникающий плазменный виток служит вторичной обмоткой импульсного трансформатора. Нагревание плазмы происходит за счет джоулева тепла, сильное продольное поле служит стабилизирующим каркасом.
Сформулированное выше условие, согласно которому для обеспечения устойчивости плазмы поле должно нарастать к периферии, не удовлетворяется в установках Токамак. Можно показать, однако, что если выполнено неравенство (4), то главные виды неустойчивости оказываются подавленными.
![]() (4)
(4)
Здесь Нz- продольное магнитное поле, Нf - магнитное поле тока, текущего через плазму, а - малый радиус тора, R - большой радиус. Действительно, при Hza/HfR= 2-3 время жизни частиц в плазменном шнуре составляет 8-10 миллисекунд. Температура плазмы составляет 1013 см-3.
Полученные параметры плазмы хотя и являются обнадеживающими, все еще сильно отличаются от тех, на которые можно было бы рассчитывать в случае идеально замагниченной плазмы. В частности, сравнительно небольшое время жизни указывает на существование неликвидированных типов неустойчивости, а следовательно, и на повышенную скорость диффузии.
Исследования на установках стеллараторного типа привели пока к более скромным результатам. Несмотря на длительность эксперимента и превосходные инженерные параметры системы, и в этом случае не удалось преодолеть неустойчивость плазмы. Диффузионные потоки на стенки во много раз превышают классические.
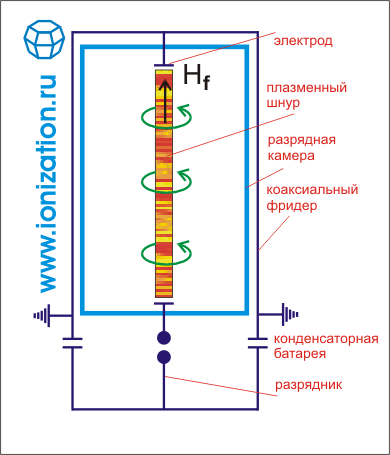
Остановимся теперь на третьем направлении поисков управляемого синтеза. Здесь функции термоизоляции и нагревания плазмы возлагаются на кратковременный импульс тока, который пропускается через разреженный дейтерий. За счет взаимодействия тока с собственным магнитным полем должно происходить сжатие плазменного шнура к оси разряда. Плазма оказывается отделенной от стенок сосуда собственным магнитным полем и должна нагреваться за счет работы сил сжатия и за счет джоулева тепла. Схема эксперимента поясняется рисунком 5. На начальной стадии исследования предполагалось, что процесс сжатия квазистационарен, что в каждый момент времени магнитное давление, сжимающее плазму, уравновешивается газовым давлением. Тогда, заменяя в (3) магнитное поле через силу тока, текущего через плазму, и принимая Тe = Тi, получим
Т = I2 / 4c2Nk (5)
где через N обозначено число частиц в сечении плазменного шнура единичной высоты. Температура вещества должна возрастать пропорционально квадрату силы тока, и численные оценки показывают, что при силе тока около 1 миллиона ампер, начальном давлении в 0,1 мм рт. ст. и диаметре сосуда в 200 мм температура плазменного шнура должна превышать 107 К. Правда, температура повысится на весьма короткое время (около 1 микросекунды), но в сильно сжатом плазменном шнуре будут происходить очень частые столкновения и можно рассчитывать на регистрацию нейтронного излучения от происходящих ядерных реакций.
В действительности картина квазистационарного сжатия оказывается грубо ошибочной. На начальной стадии процесса, после пробоя газового столба приложенным высоким напряжением, быстро нарастающий ток сосредоточивается в тонком поверхностном слое (скин-эффект). Внутренняя область столба почти не ионизована и не нагрета, газовое давление пренебрежимо мало и стягивание плазменной корочки к оси системы можно рассматривать с учетом одних сил инерции. В течение всего сжатия нет равновесия между газовым и магнитным давлением. Шнур стягивается к оси раньше, чем ток (а вместе с ним и магнитное давление) достигает максимума, но не остается в сжатом состоянии, а под действием тех же сил инерции начинает снова расширяться. Мало того, шнур неустойчив (вне шнура поле меняется как 1/r) и в результате развития макроскопических деформаций (перетяжки, изгибы) он касается стенок камеры, охлаждая и загрязняя плазму.
Замечательно, что нейтронное излучение плазмы при импульсном разряде в дейтерии все же наблюдалось. Это интересное явление было открыто группой советских физиков еще в 1952 г. Нейтронное излучение появляется не в результате нагревания всего имеющегося плазменного объема, а оказывается следствием столкновений малочисленной группы быстрых дейтонов, возникших в результате сложных ускорительных процессов в неустойчивом шнуре, с основной массой сравнительно холодной плазмы.
Увеличивая энергонапряженность системы, можно нагреть плазменный шнур до необходимых термоядерных температур к моменту первого сжатия шнура около оси и до начала развития неустойчивости. Однако для достижения условий, необходимых для получения термоядерной реакции с положительным энергетическим выходом, в предполагаемых опытах потребуется сосредоточение в импульсном разряде огромной энергии - около: 104 Мдж. Современная техника допускает сооружение импульсных установок на сотни мегаджоулей. Существуют конденсаторы, обладающие исключительно малой индуктивностью, разработаны низкоиндуктивные фидеры и весьма совершенные коммутационные устройства. Тем самым путь для дальнейшего прогресса в этом направлении открыт, но процесс приобретает характер мощного взрыва, эквивалентного по мощности взрыву нескольких тонн тротила, что совсем не похоже на плавно регулируемые управляемые термоядерные реакции.
Остановимся в заключение на возможных перспективах проводимых исследований. Работы с магнитными ловушками открытого типа характеризуются медленным, но неуклонным прогрессом в отношении параметров получаемой плазмы. Возможности усовершенствования здесь еще не исчерпаны. Вместе с тем надежды на решающий успех остаются зыбкими. Как показывают детальные расчеты, если потери частиц из ловушки всего в несколько раз превысят теоретический уровень, отвечающий полностью замагниченной теплопроводности, то осуществление термоядерного реактора с положительным энергетическим выходом становится невозможным.
Замкнутые магнитные системы представляются в настоящее время наиболее перспективными. Даже при сохранении существующего уровня потерь частиц, размер и параметры предполагаемого термоядерного реактора будущего, хотя и лежат за пределами возможностей современной техники, не кажутся безнадежными с позиций, техники ближайших десятилетий.
Развитие импульсных процессов, по-видимому, достигло естественного предела, если иметь в виду реактор в качестве конечной цели. Но дальнейшие эксперименты могут привести к построению импульсных нейтронных источников огромной мощности. Своеобразным отходом от этих исследований явилось построение систем, предназначенных для ускорения сгустков плазмы.
Статья составлена из материалов Л.А. Арцимовича А. Туктагуловым (НПФ Сапфир)
ПОЛНОЕ ИЛИ ЧАСТИЧНОЕ ЦИТИРОВАНИЕ ДАННОЙ СТАТЬИ ЗАПРЕЩЕНО




